Random Forests and Gradient Boosted Trees in TensorFlow#

June 16, 2021
tags: binary classification gradient boosted trees decision forest supervised learning

In this project/tutorial, we will

In TensorFlow version 2.5.0, support for decision trees and forests was added and announced during Google I/O 2021. The documentation, including guides, tutorials and the API reference can be found here. TensorFlow Decision Forests (TF-DF) includes the models

which we are going to explore in this tutorial.

Installation#

As of now, TensorFlow Decision Forests is not yet available on Anaconda and instead has to be installed from the Python Package Index via pip. Combining package installations via conda and pip should be done with a certain level of care. Following spellbook’s typical setup specified in spellbook.yml and combining the normal conda-based TensorFlow installation with TF-DF installed via pip will most probably not work. Instead, we are going to create a separate conda environment spellbook-no-tensorflow just for this tutorial and install both TensorFlow and TF-DF via pip using the provided requirements.txt.

So let’s roll:

$ cd examples/2-tensorflow-decision-forests

If the default spellbook conda environment is currently active, deactivate it

$ conda deactivate

and create the dedicated environment excluding TensorFlow

$ conda env create --file spellbook-no-tensorflow.yml

Once this is done, activate it and use pip to install both TensorFlow and TensorFlow Decision Forests into the new conda environment spellbook-no-tensorflow

$ conda activate spellbook-no-tensorflow
$ pip install -r requirements.txt

Parallel Coordinate Plots#

This tutorial uses Kaggle’s Stroke Prediction Dataset, just like the Binary Classification with the Stroke Prediction Dataset project before. So therefore, before we try out the decision trees in TF-DF, let’s have a look at another possibility of visualising entire datasets in a rather compact way - parallel coordinate plots. In spellbook, they are implemented in spellbook.plot.parallel_coordinates() and can be used like this:

fig = sb.plot.parallel_coordinates(data.sample(frac=1.0).iloc[:500],
   features, target, categories)
sb.plot.save(fig, 'parallel-coordinates.png')

We first shuffle the datapoints using pandas.DataFrame.sample() and then take the first 500 of them in order to get a representative subset of all patients. The resulting plot is shown in Figure 1.

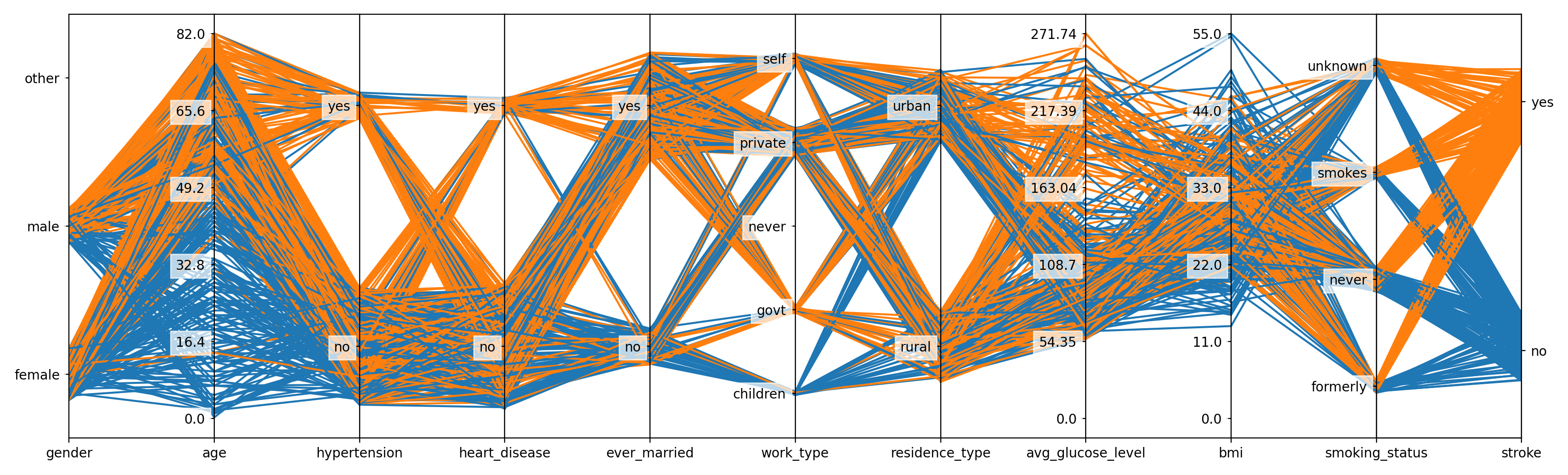
../../_images/parallel-coordinates1.png

Figure 1: Parallel coordinates plot showing a subset of Kaggle’s Stroke Prediction Dataset#

We can see the binary categorical target variable stroke on the far right-hand side of the plot. Patients with a stroke are shown with orange lines and patients without a stroke with blue lines. The features are shown in individual coordinate axes left of the target. There are both continuous variables, such as age or bmi, and categorical variables, such as gender or heart_disease and the density of the lines indicates the prevalence of the target labels. Looking at the age of the patients, we can see that strokes are more present at higher ages. For categorical variables, the datapoints are randomly smeared or shifted around the respective categories or classes. Therefore, the lines are not all drawn exactly on top of each other and it is possible to get an impression of the composition of the datapoints in a certain category in terms of the target labels. For instance, we can see that the no classes of the variables hypertension and heart_disease contain significant fractions of patients both with and without strokes, while the yes categories seem to be enriched in stroke patients. This seems plausible as it indicates positive correlations between these conditions and the presence of strokes. Additionally, the size of the smearing or shifting interval is chosen in proportion to the number of datapoints in the respective categories. Therefore, it is possible to get a feeling for how many patients fall into which class for each feature. For example, we can see that more patients work in the private sector that for the government.

Random Forest#

Just like regular TensorFlow, TF-DF implements the Keras API and therefore, we can follow very closely what we did in Binary Classification with the Stroke Prediction Dataset. So now let’s start using TF-DF and begin with the random forest model:

# data loading and cleaning
data, vars, target, features = helpers.load_data()

# inplace convert string category labels to numerical indices
categories = sb.input.encode_categories(data)

# oversampling (including shuffling of the data)
data = sb.input.oversample(data, target)

# split into training and validation data
n_split = 7000
train = tfdf.keras.pd_dataframe_to_tf_dataset(
    data[features+[target]].iloc[:n_split], label=target)
val = tfdf.keras.pd_dataframe_to_tf_dataset(
    data[features+[target]].iloc[n_split:], label=target)

After loading the Stroke Prediction Dataset with the helper function, we apply oversampling to counteract the imbalance in the target classes between the 4.3% of the patients with a stroke and the overwhelming majority of 95.7% without a stroke. The dataset and the method of oversampling are described in detail in Binary Classification with the Stroke Prediction Dataset. Finally, we split the dataset into a training and a validation set using TF-DF’s tfdf.keras.pd_dataframe_to_tf_dataset.

Note that we hardly did any preprocessing - in particular, decision trees do not need normalised data. Likewise, it is not necessary to turn categorical variables expressed by strings or integers into properly indexed pandas.Categoricals. This is only needed here for the oversampling to work - but not for the decision trees.

Next, we prepare a range of metrics useful for binary classification - the same ones that are also used and described in Model Training and Validation. Afterwards, we instantiate a tfdf.keras.RandomForestModel, sticking to the default values. We add the metrics using the compile method and train the model with model.fit on the training dataset train. Finally, we save the model so that it can be reloaded and used again later:

# define binary metrics
metrics = [
    tf.keras.metrics.BinaryCrossentropy(name='binary_crossentropy'),
    tf.keras.metrics.BinaryAccuracy(name='accuracy'),
    tf.keras.metrics.TruePositives(name='tp'),
    tf.keras.metrics.TrueNegatives(name='tn'),
    tf.keras.metrics.FalsePositives(name='fp'),
    tf.keras.metrics.FalseNegatives(name='fn'),
    tf.keras.metrics.Recall(name='recall'),
    tf.keras.metrics.Precision(name='precision')
]

# prepare and train the model
model = tfdf.keras.RandomForestModel()
model.compile(metrics=metrics)
model.fit(train)
# model.summary()
model.save('model-{}'.format(prefix))

By default, tfdf.keras.RandomForestModel uses 300 trees with a depth of up to 16 and fitting our training dataset only takes a few seconds. The rapid way of evaluating the model performance goes somewhat like this:

eval = model.evaluate(val, return_dict=True)
print('eval:', eval)

eval is a dict containing the values of the metrics calculated from the validation dataset.

But let’s go on and calculate the confusion matrix:

# separate the datasets into features and labels
train_features, train_labels = zip(*train.unbatch())
val_features, val_labels = zip(*val.unbatch())

# obtain the predictions of the model
train_predictions = model.predict(train)
val_predictions = model.predict(val)

# not strictly necessary: remove the superfluous inner nesting
train_predictions = tf.reshape(train_predictions, train_predictions.shape[0])
val_predictions = tf.reshape(val_predictions, val_predictions.shape[0])

# until now the predictions are still continuous in [0, 1] and this breaks the
# calculation of the confusion matrix, so we need to set them to either 0 or 1
# according to an intermediate threshold of 0.5
train_predicted_labels = sb.train.get_binary_labels(
    train_predictions, threshold=0.5)
val_predicted_labels = sb.train.get_binary_labels(
    val_predictions, threshold=0.5)

# calculate and plot the confusion matrix
class_names = list(categories['stroke'].values())
class_ids = list(categories['stroke'].keys())
val_confusion_matrix = tf.math.confusion_matrix(
    val_labels, val_predicted_labels, num_classes=len(class_names))
sb.plot.save(
    sb.plot.plot_confusion_matrix(
        confusion_matrix = val_confusion_matrix,
        class_names = class_names,
        class_ids = class_ids),
    filename = '{}-confusion.png'.format(prefix))

Just like in Model Training and Validation, we can also plot normalised versions of the confusion matrix. The confusion matrix with the absolute datapoint numbers is given in Figure 2 and a version where each true label/class is normalised in Figure 3:

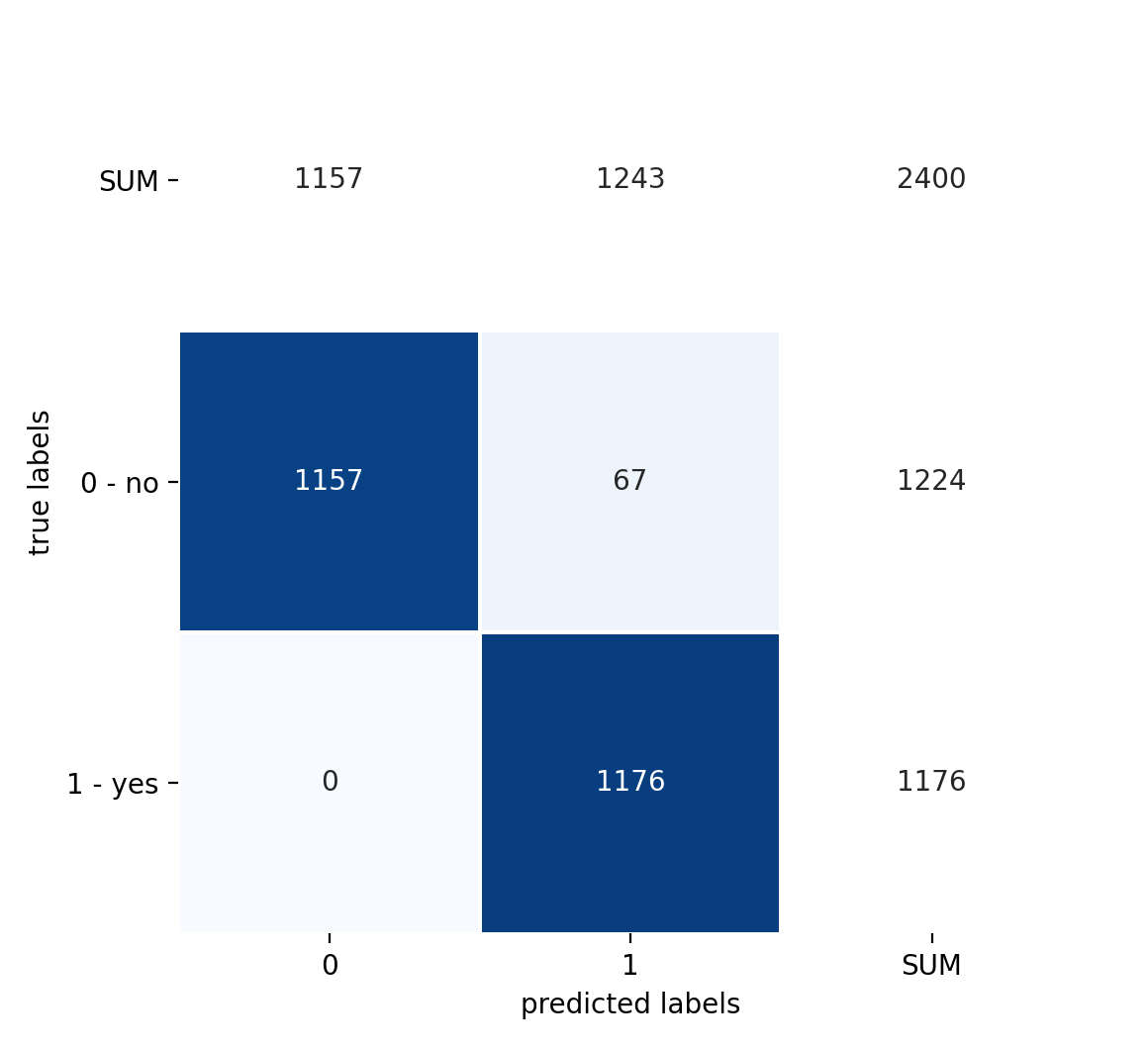
../../_images/random-forest-confusion.png

Figure 2: Confusion matrix with absolute datapoint numbers#
../../_images/random-forest-confusion-norm-true.png

Figure 3: Confusion matrix normalised along each true label/class#

We can see that already with the default forest configuration, the model’s performance is good enough to not produce any false negatives. As for the false positives, only 5.5% of the truly negative datapoints are wrongly classified as positive.

Gradient Boosted Trees#

Random forests consist of many trees, each trained on a randomly drawn subset of the full training dataset. In contrast, a boosted decision trees model consists of many trees, where after training one tree, the weights of the wrongly classified datapoints are increased before training the next tree. This way, increasingly more importance is puts on datapoints that are hard to classify.

The only real change we have to make to use a gradient boosted trees model is in the instantiation:

model = tfdf.keras.GradientBoostedTreesModel()

By default, TF-DF trains up to 300 trees with a depth of up to 6.

The resulting confusion matrices are shown in Figure 4 and 5:

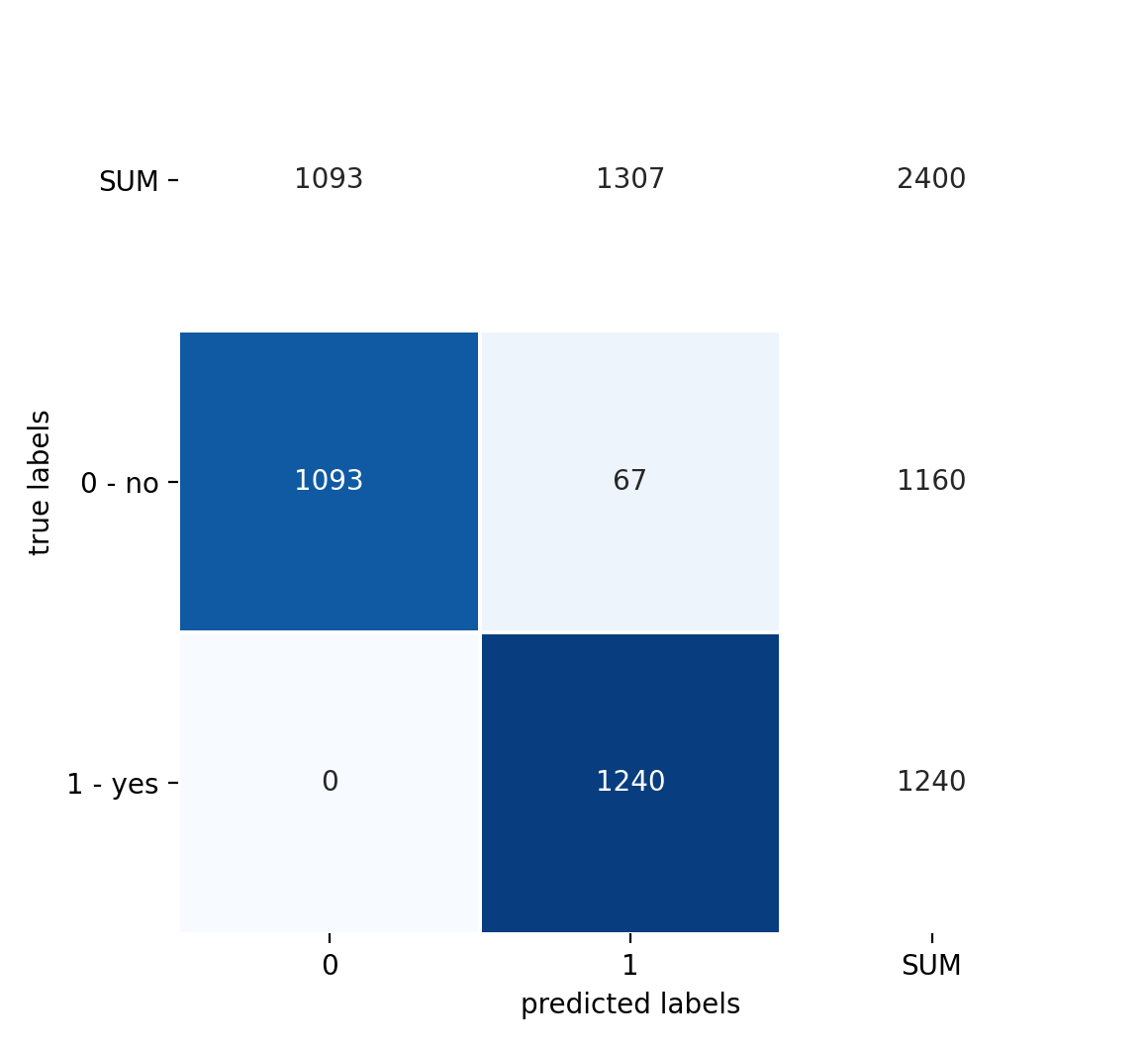
../../_images/gradient-trees-confusion.png

Figure 4: Confusion matrix with absolute datapoint numbers#
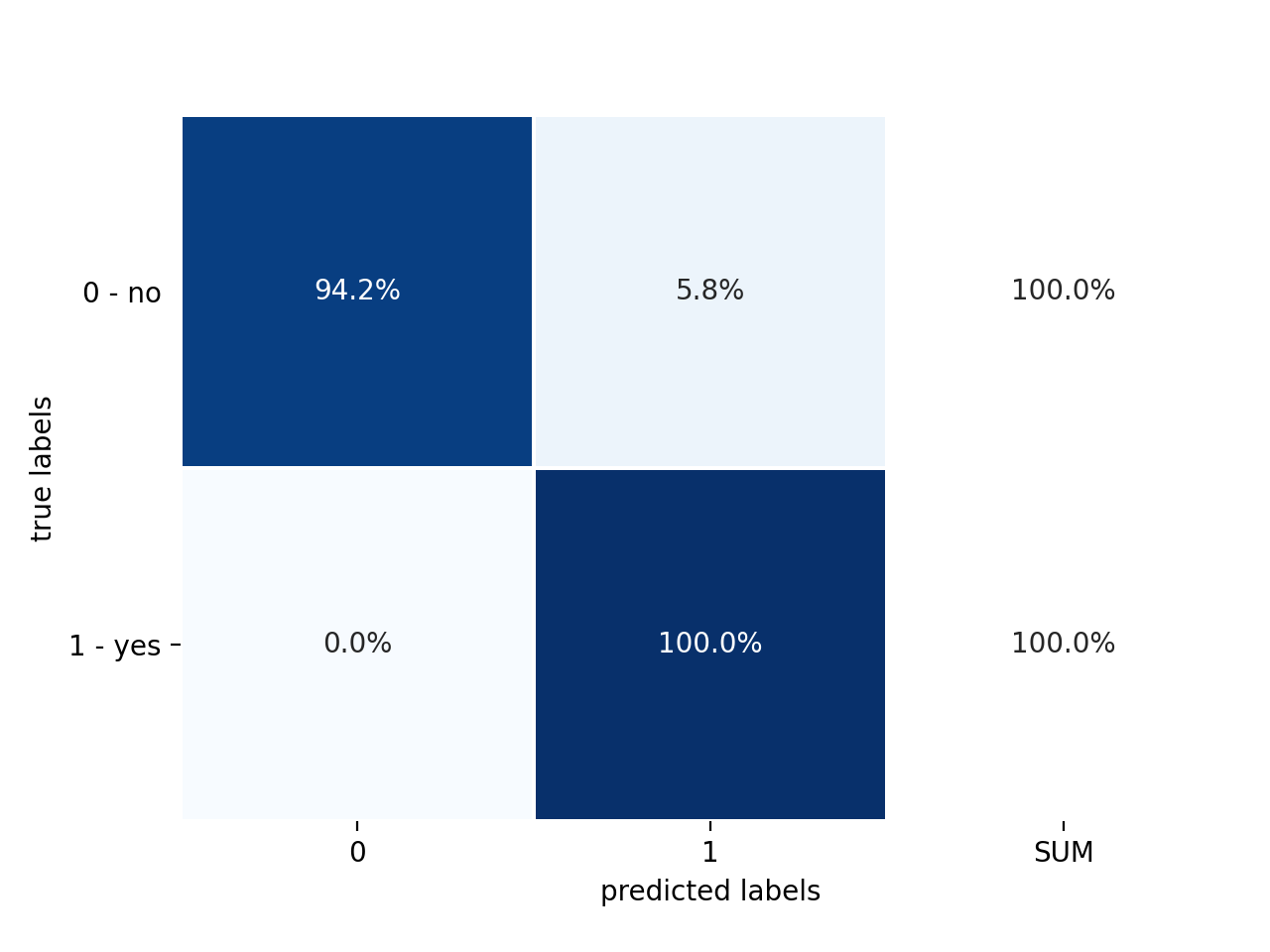
../../_images/gradient-trees-confusion-norm-true.png

Figure 5: Confusion matrix normalised along each true label/class#

We can see that the performance is very similar to the random forest, with a false positive rate (FPR) of 5.8%.

Before we go on to compare the different tree models and the final neural network classifier trained in Binary Classification with the Stroke Prediction Dataset, let’s have a look at a model-agnostic way of determining the importance that each feature plays in the performance of the classifier: the permutation importance. While one or more input features cannot simply be removed, the idea behind permutation importance is to break the correlation of a feature with the target by randomly permuting the values of just that particular feature - hence the name. This way, the classifier is no longer able to use that feature when deriving the prediction. Permutation importance is implemented in spellbook in spellbook.inspect.PermutationImportance, based on sklearn.inspection.permutation_importance(), and can be calculated and plotted as follows for any of the metrics previously defined and passed to the model in the compile step:

importance = sb.inspect.PermutationImportance(
   data, features, target, model, metrics, n_repeats=10, tfdf=True)
sb.plot.save(
   importance.plot(
      metric_name='accuracy',
      annotations_alignment = 'left',
      xmin = 0.62),
   filename='{}-permutation-importance-accuracy.png'.format(prefix))

resulting in the plot shown in Figure 6:

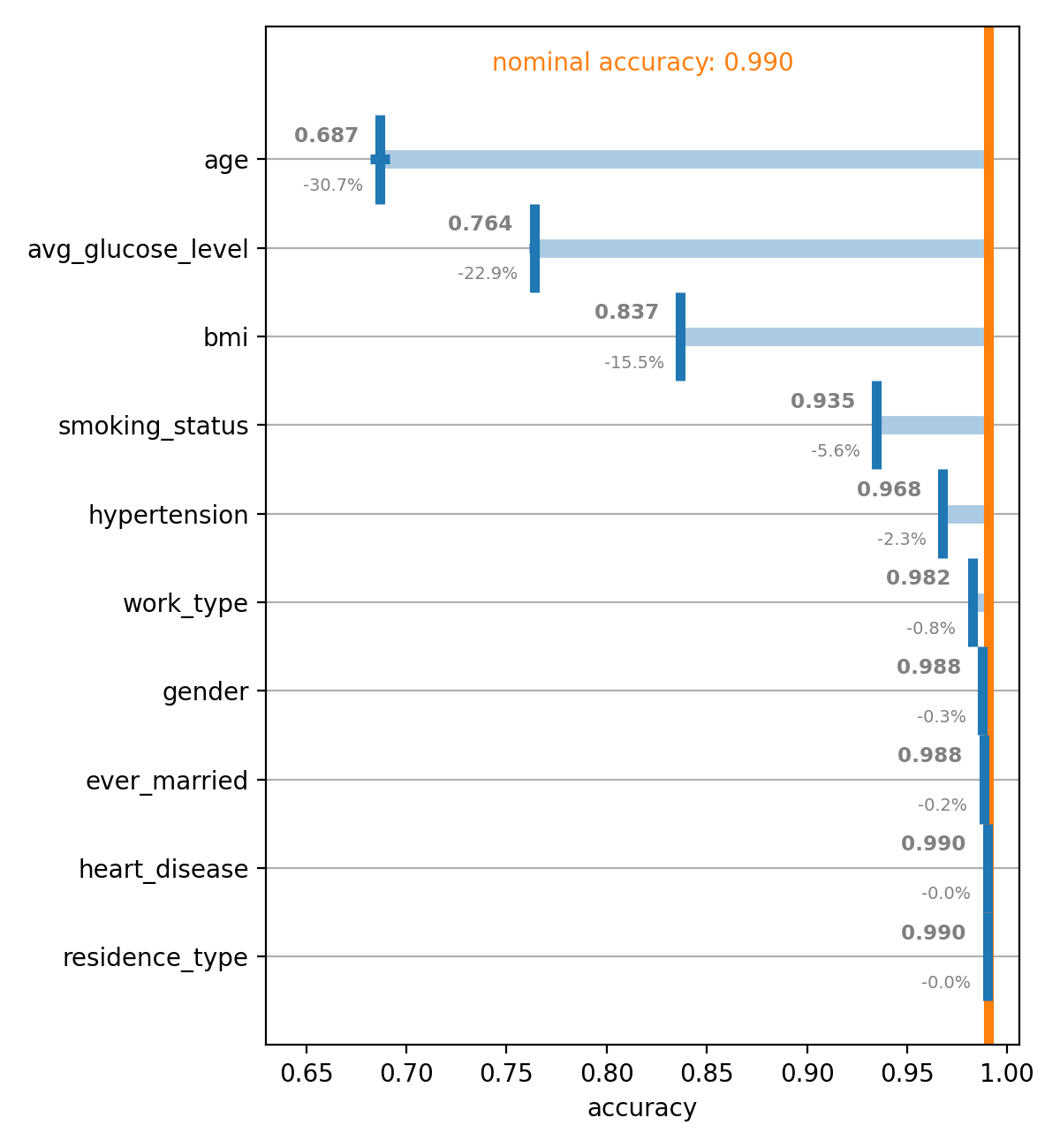
../../_images/gradient-trees-permutation-importance-accuracy.png

Figure 6: Permutation importance#

We can see to what values the metric, in this case the classification accuracy, decreases when each one of the feature variables is randomly permuted. Each feature is permuted n_repeats times and the average and standard deviation of the resulting metrics are calculated. The standard deviations are used to draw horizontal error bars on the average deteriorated metrics, but can also be printed into the plot.

We can see that the gradient boosted trees classifier relies most heavily on age, the average glucose level and the BMI, with the accuracy dropping by about 31%, 23% and 16%, respectively, when the corresponding values are scrambled.

While the approach behind permutation importance is model-agnostic, care has to be taken in interpreting the results when some of the features are correlated. In this case, information from the missing permuted feature can at least partly be recovered by the classifier from the remaining correlated variable(s), leading to a less-than-expected deterioration of the studied metric. To overcome this limitation, spellbook.inspect.PermutationImportance provides a mechanism for grouping multiple features into clusters and permuting them simultaneously.

Further info:

Comparison Against Neural Networks#

Finally, let’s compare our tree classifiers against the final neural network classifier trained at the end of Binary Classification with the Stroke Prediction Dataset using both oversampling and input normalisation and have a look at the different Receiver Operator Characteristic (ROC) curves:

import spellbook as sb

# load the pickled ROC curves of the different models
roc_network = sb.train.ROCPlot.pickle_load(
    '../1-binary-stroke-prediction/oversampling-normalised-e2000-roc.pickle')
roc_forest = sb.train.ROCPlot.pickle_load('random-forest-roc.pickle')
roc_trees = sb.train.ROCPlot.pickle_load('gradient-trees-roc.pickle')

# add and style the ROC curves
roc = sb.train.ROCPlot()
roc += roc_network
roc.curves['oversampling normalised / 2000 epochs (validation)']['line'].set_color('black')
roc.curves['oversampling normalised / 2000 epochs (training)']['line'].set_color('black')
roc += roc_trees
roc.curves['gradient trees (validation)']['line'].set_color('C1')
roc.curves['gradient trees (training)']['line'].set_color('C1')
roc += roc_forest

# calculate and draw the working points with 100% true positive rate
WPs = []
WPs.append(roc.get_WP(
    'oversampling normalised / 2000 epochs (validation)', TPR=1.0))
WPs.append(roc.get_WP(
    'gradient trees (validation)', TPR=1.0))
WPs.append(roc.get_WP(
    'random forest (validation)', TPR=1.0))
roc.draw_WP(WPs, linecolor=['black', 'C1', 'C0'])

# save the plot
sb.plot.save(roc.plot(xmin=-0.2, xmax=11.0, ymin=50.0), 'roc.png')

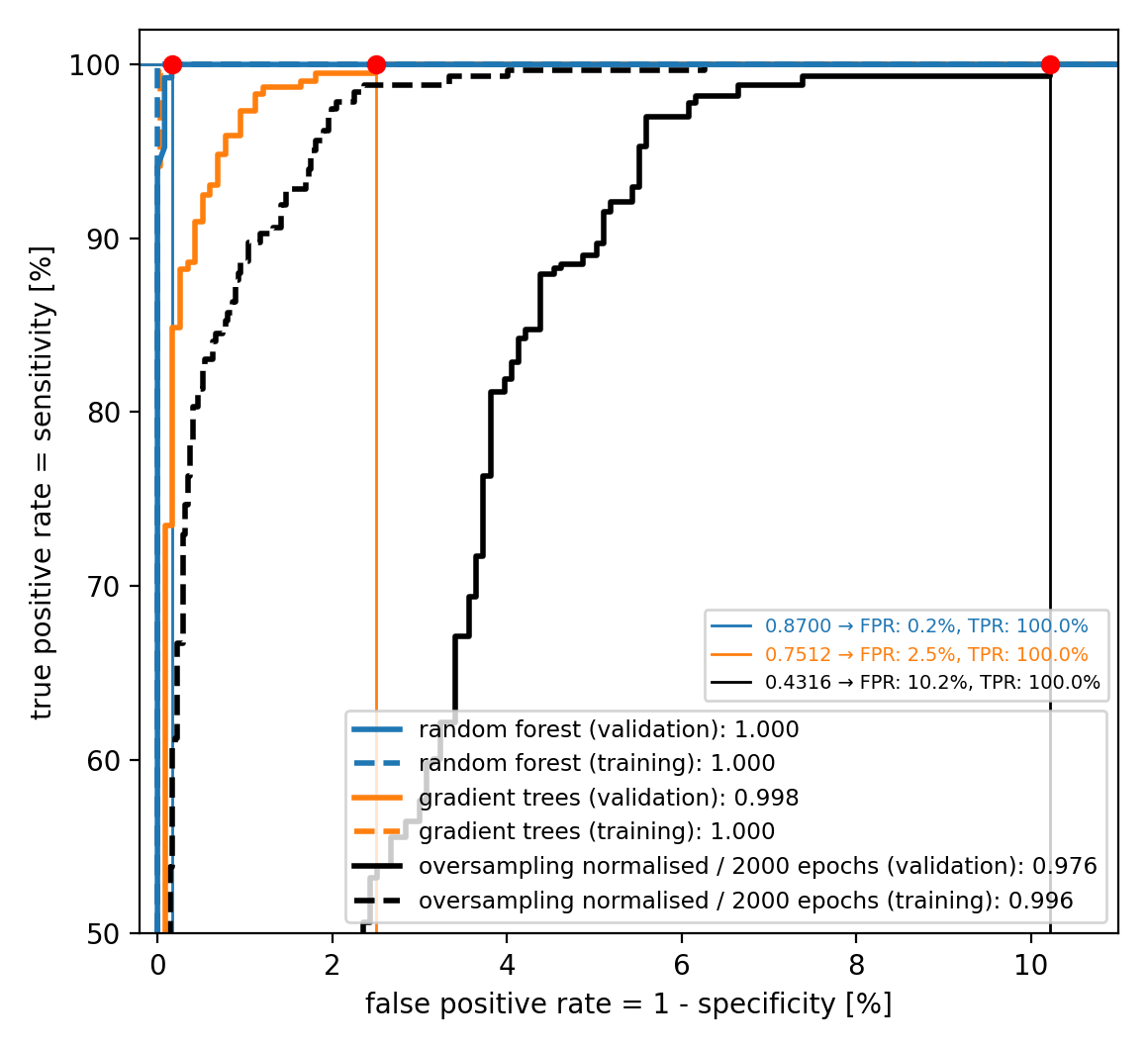
The resulting ROC curves with the working points at 100% true positive rate (TPR) indicated are shown in Figure 7.

../../_images/roc1.png

Figure 7: Receiver Operator Characteristic (ROC) curves#

There, we can see that both the decision forest and the gradient boosted trees outperform the neural network model, reaching lower false positive rates (FPR) of 0.2% and 2.5%, respectively, while maintaining 100% TPR. Let’s also keep in mind that this is not only without any hyperparameter tuning but even just using the defaults. Furthermore, while it took about an hour to train the neural network classifier on a fairly standard laptop, fitting the decision tree models was a matter of a few seconds.

This illustrates that decision trees tend to prefer structured data, i.e. data showing its characteristic patterns when represented in a table with the features in the columns and each datapoint in a row. While images, being a typical example of unstructured data, can also be represented in such a tabular manner, with each pixel in its own column, this is not a representation geared towards showing the characteristic patterns - which can e.g. move across the image and therefore from some columns to others. Neural networks are better at identifying and learning the relevant patterns in such unstructured datasets.