spellbook.inspect

Functions for model inspection

Classes:

PermutationImportance(data, features, ...[, ...])

Feature importance from permutation

Classes

PermutationImportance

class spellbook.inspect.PermutationImportance(data, features, target, model, metrics, n_repeats=10, feature_clusters=None, tfdf=False)

Feature importance from permutation

This implementation follows the Permutation Feature Importance algorithm in scikit-learn

• presented in the scikit-learn User Guide

• implemented in sklearn.inspection.permutation_importance()

but goes further in that it provides a mechanism for permuting clusters of multiple features simultaneously. This allows to estimate the permutation importance when some of the feature variables are correlated.

Parameters

• data (pandas.DataFrame) – The dataset

• features – The names of the feature variables

• target – The name of the target variable

• model (tf.keras.Model) – The predictor/classifier/regressor

• metrics ([tf.keras.metrics.Metric]) – The metrics to evaluate

• n_repeats (int) – How often each feature (cluster) is permuted

• feature_clusters (typing.Optional[typing.Dict[str, typing.List[str]]]) – Optional. Dictionary with cluster names as keys and lists of features as the values. Each list contains the features that are grouped together as one cluster and permuted simultaneously.

• tfdf (bool) – Optional. Whether or not the model is one of the models in tensorflow_decision_forests

baseline

Dictionary containing the nominal metrics, i.e. without permutation. The keys are the names of the metrics and the values are the values of the metrics.

Type

dict[str, float]

results

For each feature or feature cluster, a dictionary is added to the list. Each dictionary has the following keys and associated values:

• feature: The name of the feature or the feature cluster

• results: A list containing a dictionary for each permutation. Each dictionary contains the names and values of the metrics calculated in that permutation

• mean: A dictionary containing the means of the results, with one entry for each metric

• std: A dictionary containing the standard deviations of the results, with one entry for each metric

• mean_rel_diff: A dictionary containing the relative differences between the mean and the nominal, with one entry for each metric

Type

list[dict]

tfdf

Whether or not the model is one of the models in tensorflow_decision_forests

Type

bool

See also

• scikit-learn example: Permutation Importance with Multicollinear or Correlated Features

Methods:

__init__(data, features, target, model, metrics)
plot(metric_name[, xmin, xmax, ascending, ...])	Plot the permutation importance of features / feature clusters

__init__(data, features, target, model, metrics, n_repeats=10, feature_clusters=None, tfdf=False)

plot(metric_name, xmin=None, xmax=None, ascending=True, annotations_alignment='left', show_std=False, show_rel_diffs=True, rainbow=False)

Plot the permutation importance of features / feature clusters

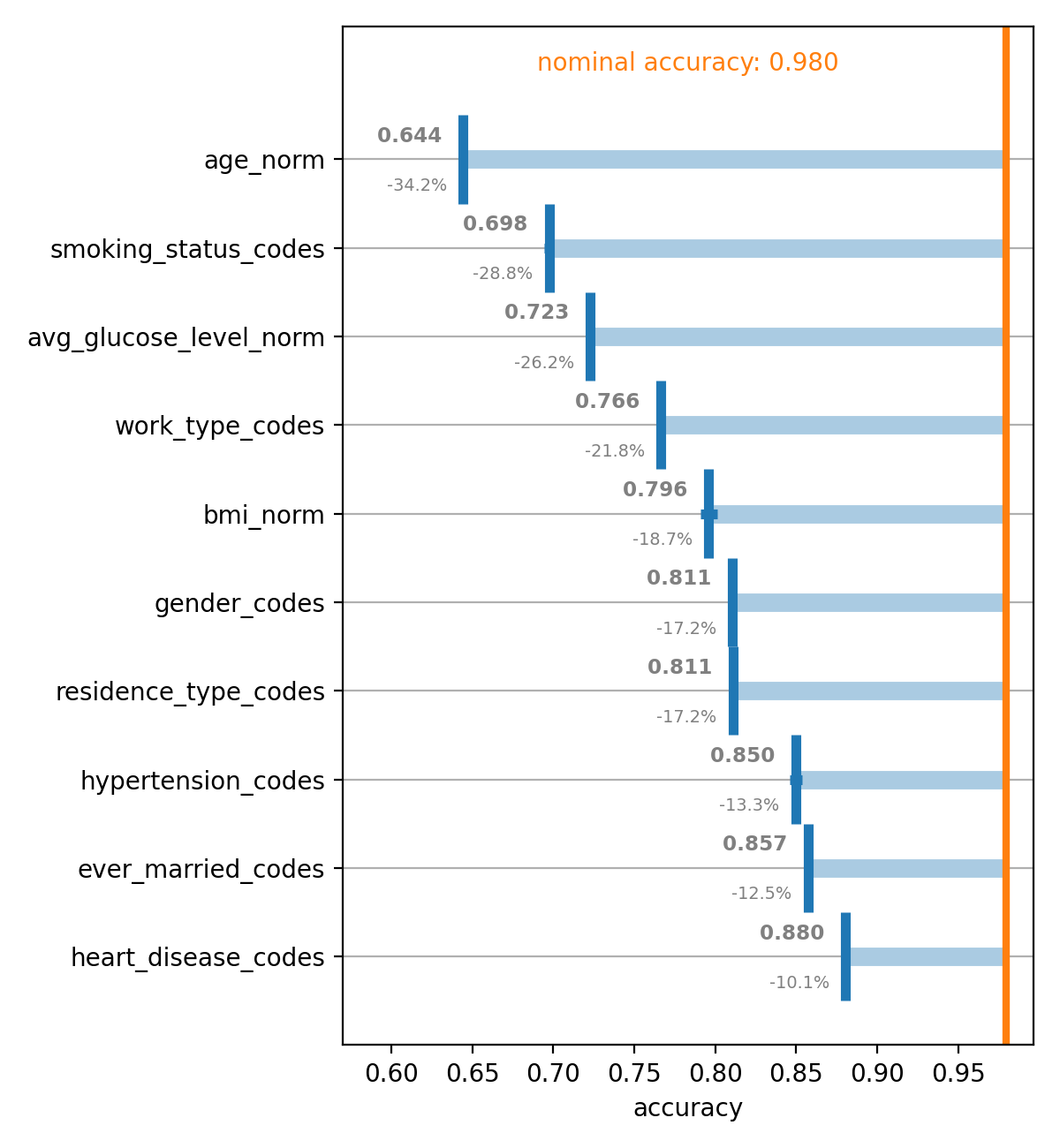
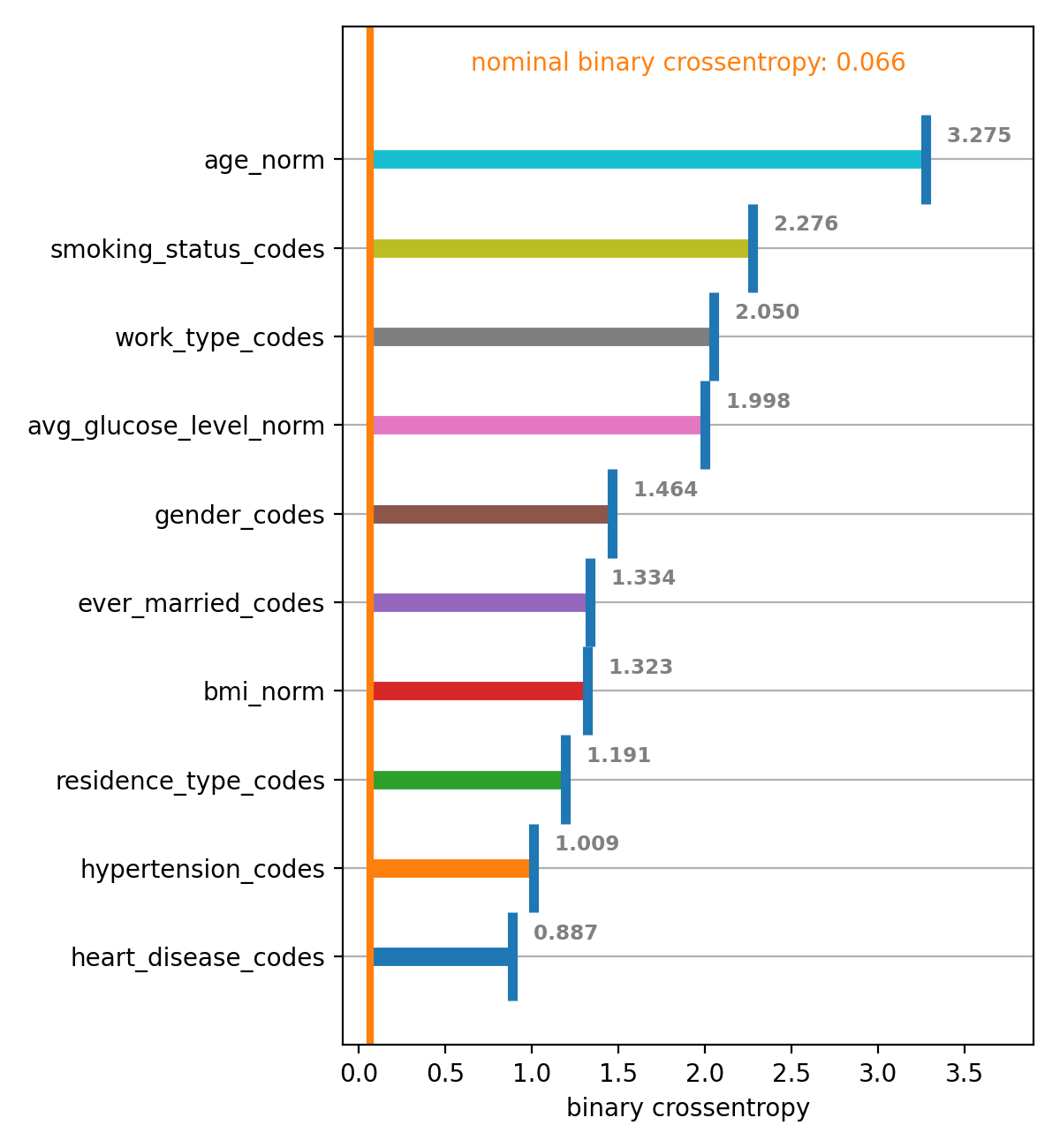
Parameters

• metric_name – The name of the metric to be plotted

• xmin (typing.Optional[float]) – Optional. The lower end of the x-axis

• xmax (typing.Optional[float]) – Optional. The upper end of the x-axis

• ascending (bool) –

  Optional. Order from the top to the bottom of the plot:

  • True: Ascending from smaller to larger values

  • False: Descending from larger to smaller values

• annotations_alignment (str) – Optional. Whether the annotations indicating the mean (and possibly the standard deviation) as well as the relative difference to the nominal metric should be printed to the left or the right of the markers.

• show_std (bool) – Optional. Whether or not the standard deviations of the metrics for the permuted features should be included in the annotations.

• show_rel_diffs (bool) – Optional. Whether or not the relative differences between the mean of the metrics for the permuted features and the nominal metric shown be included in the annotations.

• rainbow (bool) – Optional. Whether or not the horizontal bars between the means of the metrics for the permuted features and the nominal metric should cycle through the colour palette.

Return type

matplotlib.figure.Figure

Returns

The figure containing the ranking of the features according to their permutation importance